Choosing the Right Finite Element | MSC Nastran

MSC Nastran contains a large library of structural elements. In many situations several elements are capable of modeling the same structural effects. The criteria for the selection of an element may include its capabilities (for example, whether it supports anisotropic material properties), its cost (in general, the more DOF an element has, the more expensive it is), and/or its accuracy.

In this context, it is critical that you have a fairly good idea of how the structure will behave prior to generating your finite element model. The best source of such insight is usually experience with similar structures. In other words, understanding the load path is crucial in the selection of the appropriate element. In addition, a few hand calculations can usually provide a rough estimate of stress intensities. Such calculations are always recommended. If you do not have a fairly good idea of how the structure will behave, you may be misled by incorrect results due to errors or incorrect assumptions in your input data preparation.

The following guidelines are provided to help you in selecting the “right” element for your task.

General Guidelines

Always experiment with a small test model when using elements that you are not familiar with. This practice is cheaper than experimenting with a large production model, and it gives you a better understanding of an element’s capabilities and limitations prior to applying it to a large production model.

Zero-Dimensional Elements

When you use CELASi elements to represent concentrated springs between two components of translation, the directions of the two components must be coaxial. Even small deviations in direction can induce a significant moment to your model that does not exist in your physical structure. It is recommended that when a CELASi element is used, the locations of the two end points be coincident in order to avoid this type of problem. If the two end points are not coincident, you should consider using a CROD or CBUSH element instead.

One-Dimensional Elements

If only an axial and/or torsion load is to be transmitted in an element, then the CROD is the easiest element to use.

A CBAR is easier to use than a CBEAM element. The I1 and/or I2 values can be set to zero.

Use the CBEAM element instead of the CBAR element if any of the following features is important:

• The cross-sectional properties are tapered.
• The neutral axis and shear center do not coincide.
• The effect of cross-sectional warping on torsional stiffness is critical.
• The difference in the mass center of gravity and the shear center is significant.

The formulation for the CBEAM element is based on a flexibility approach; the element stiffness matrix is generated by inverting the flexibility matrix. For this reason, I1 and I2 must not be zero for the CBEAM element.

CBEAM3 elements favor a structure with initial curvatures and with high order shell elements.

Two-Dimensional Elements

In general, quadrilateral elements (CQUAD4 and CQUAD8) are preferred over the triangular elements (CTRIA3 and CTRIA6). The CTRIA3 element is a constant strain element. It is excessively stiff, and when used alone, it is generally less accurate than the CQUAD4 element, particularly for membrane strain. Whenever feasible, the CQUAD4 element should be used instead of the CTRIA3 element. CTRIA3 should only be used when necessary for geometric or topological reasons, for example, mesh transition between regions of quadrilateral elements with different meshes or near the polar axis of a spherical shell.

Avoid using CTRIA3 in locations where the membrane stresses are changing rapidly, for example, in the web of an I-beam. Since CTRIA3 has constant membrane stresses, a large number of them may be needed to obtain acceptable accuracy. It is better to use quadrilateral elements or CTRIA6 elements, if possible.

Do not use plate or shell elements (CQUADi, CTRIAi) in stiffened shell structures with very thin panels that can buckle. Shear panels (CSHEAR) should be used in this case or in any situation where direct stresses cannot be supported, such as in a very thin curved panel.

Avoid highly skewed elements (see Figure 9-1). The angle α should be as close to 90 degrees as possible.

 

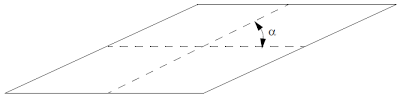Figure 9-1 Highly Skewed Element

 

For the CTRIA3 element, the skew test is based upon the three vertex angles.

Aspect ratio is defined as l / ω (length/width). Very high aspect ratio (see Figure 9-2) should also be avoided, although it is no longer true that accuracy degrades rapidly with aspect ratios as it once did with some of the obsolete elements.

 

Figure 9-2 Element with High Aspect Ratio

 

Warping is a measure of the amount the element deviates from being planar (see Figure 9-3). Element warping should be minimized.

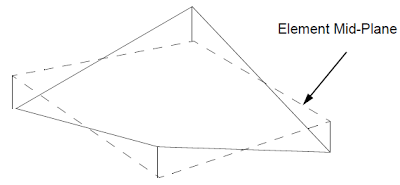Figure 9-3 Highly Warped Element

 

For the CQUAD8 elements, if midside nodes are present, they should be located within the middle third of the edge. If a midside node is located at one-fourth the distance of the edge as measured from either corner node on the edge, the internal strain field becomes singular at the corners of the element. For best results, it is recommended that the midside node be located as close to the center of the edge as possible. If midside nodes are desired, the general recommendation is to include all of them. A CQUAD8 element with midside nodes deleted is excessively stiff and therefore is inferior to a CQUAD4 element.

Figure 9-4 CQUAD8 with Missing Midside Node

 

For single curved structures (e.g., a cylinder), the CQUAD8, in general, yields better results than the CQUAD4 element. For doubly curved structures (e.g., a spherical dome), the CQUAD4 element, in general, performs better than the CQUAD8 (see Reference 15.).

The shell normal (param,snorm,x) should be turned on when using the CQUAD4, CTRIA3, CQUADR, or CTRIAR element. See Shell Normals, 353 for further details.

The membrane properties for the CQUADR and CTRIAR elements are less sensitive to the element shape than the CQUAD4 and CTRIA3. The CQUADR and CTRIAR elements can be used in conjunction with each other, but not with other elements.

An increase in accuracy can be expected when using the QUADR element vs the QUAD4 element, particularly in areas of the model that are more coarsely meshed.

Existing QUAD4 element models can easily be converted to QUADR elements by setting System Cell (QRMETH (370)) in the NASTRAN Statement. QRMETH=5 will convert all QUAD4/TRIA3 elements in the model to QUADR/TRIAR.To show the difference in accuracy between the QUADR and QUAD4 elements, four mesh densities for a simple “T-Section” test model were run using MSC Nastran. von Mises stress results, taken at a central position in the “T-Section”, were compared and they showed the QUADR was more consistant and accurate as the density was reduced. See Figure 9-5.

Figure 9-5

 

Shell Normals

By default, the direction of the normal rotation vector for flat plate elements is assumed to be perpendicular to the plane of each element. If the model is curved, the shell bending and twist moments must change direction at the element intersection. If transverse shear flexibility is present, the deformations may be too large. (Because elements using low-order formulations ignore the edge effect, this rarely causes any problems-the default value of 100 on the parameter K6ROT partially cures the problem.) With the unique normal (SNORM) option, the rotational degrees of freedom at each corner of an element are measured relative to the specified normal vector direction. Thus, all elements connected to a grid point will use a consistent direction for defining shell bending and twisting moments.

In CQUAD4 and CTRIA3 elements, the stiffness matrices of the elements are modified to eliminate the undesirable small stiffness in the rotational motions about the shell normal vector. In effect, the transformation replaces the normal moments with in-plane forces. No changes were made to the basic element stiffness matrix, and therefore flat plate models will not be affected. The objective of the new transformation was to remove a potential weakness in curved shell models and allow the automatic constraint process to remove the true singularity in the assembled stiffness matrix.

The CQUADR and CTRIAR elements are also improved for some types of shell problems. Because of their extra degrees of freedom, these elements are more sensitive to the coupling between in-plane and out-of-plane motion due to curvature. This formulation of using a common unique normal, provides more consistency between adjacent elements in a curved shell.

Shell normals are available for CQUAD4, CQUADR, CTRIA3, and CTRIAR elements. Normals are activated if the actual angle between the local element normal and the unique grid point normal is less than , the default value for β (see Figure 9-6.) The default β for can be changed by setting PARAM,SNORM, β to the desired real value up to 89 degrees. The unique grid point normal is the average of all local shell element normals at a specific grid point. Generated grid point normals may be overwritten by user-defined normals.

Figure 9-6 Unique Grid Point Normal

 

A shell normal defines a unique direction for the rotational degrees of freedom of all adjacent elements. A shell normal vector is created by averaging the normal vectors of the attached elements. If the actual angle is greater than the value defined on PARAM,SNORM, (default = 20.) the edge is assumed to be a corner, and the old method is used. Shell normals improve the accuracy of the results in curved shells where in-plane shear and twisting moments act together.

If the actual shell normal vector is known, such as in a cylinder or sphere, the automatically calculated values may be superseded by the actual vectors using the Bulk Data entry

 

where GID is a unique grid point, CID is the coordinate system for defining the shell normal vector and V1, V2, and V3 are unscaled components of the vector in the coordinate system.

A second parameter, SNORMPRT, controls the print or punch of values of the internal shell normals. The output format is the same as the SNORM Bulk Data so that the individual values may be used and modified on a subsequent job.

Remarks and Recommendations

The following remarks are applicable to the shell normal option:

1. The type of structure that exhibits the most change in results is a thick curved shell with large inplane shear forces and twisting moments.
2. Most other problems, such as flat plates and curved shells with pressure loads, show changes in results of less than 1%. More degrees of freedom may be constrained using this improved formulation. This formulation results in zero in-plane rotational stiffness values.
3. It has been observed from testing that the automatic normal vector calculations produced answers nearly equal to and as accurate as those using the explicit SNORM vector input. In other words, the results were insensitive to small differences in the direction of the vectors. The important fact is that the shell normal vector requires the connected elements to use a consistent normal direction.
4. The CQUAD8 and CTRIA6 elements are not included in the shell normal processing. If they are modeled correctly, they do not require shell normal processing. Connecting these elements to the lower-order flat elements is not recommended.
5. Curved shell elements have no stiffness in the rotational degree of freedom when the formulation is used-consequently, mechanisms may be introduced. Mechanisms occur when elements, RBEs, or MPCs are connected to the out-of-plane rotation of the shell grid points. Note that PARAM,AUTOSPC,YES does not constrain these mechanisms.
6. In linear solution sequences, the values of “param,k6rot,100.” and “param,snorm,20.” are the default.
7. Transverse shear flexibility (MID3 on the PSHELL property entry) should be left on when normals are used.

Three-Dimensional Elements

Although the CHEXA and CPENTA elements are designed to behave reasonably well as thin shell elements, it is recommended that they not be used in this capacity. The high ratio of extensional stiffness in the direction normal to the effective transverse shear stiffness can produce significant round-off errors.

As in the case of plate elements, if midside nodes are present for the solid elements, they should be located as close to the center of the edge as possible. Again, if midside nodes are desired, the general recommendation is to include all of them.

R-Type Elements

A high degree of precision must be maintained when specifying coefficients for MPCs in order to avoid introduction of unintentional constraints to rigid body motions. Rigid elements (e.g., the RBE2, RBAR, etc.) should be used whenever possible because their constraint coefficients are internally calculated to a high precision. Furthermore, these R-type elements require much less user interaction. The weld family of elements offer excellent ways of modeling structural connections.

All of the content in this blog post has been directly extracted from Chapter 9 of the MSC Nastran 2012 Linear Static Analysis User's Guide.